python 数据处理基础之 numpy 的通用函数

发表于 分类于 ， 阅读次数： ：

numpy 提供了一系列的函数来方便对ndarray进行操作，这些函数基本上都有2个特点：

  1. 执行效率高；
  2. 元素级操作（即对数组中每个元素都进行运算操作）

这也就是说，当遇到此类需求时，使用 ufunc 可以提供高效而又方便的操作，日常进行数据处理时应该常用。

比如，对数组内的每个元素求平方根：

对数组内的每个元素求平方根
1
2
arr = np.arange(3)  # [0 1 2]
np.sqrt(arr)        # [0 1 1.41421356]

1 导图

(建议看每一章时，先把此导图打印出来对着看，好让自己对整体内容有个大概的把握与知道自己学习到哪个位置：）我自己做此笔记也是这样，把导图都打印出来，然后对着自己的笔记回顾，看完哪里就去哪里打个勾表示复习过一遍了)

2 基本运算

3 通用ufunc

ufunc中的各种方法其实都是一眼明了的(像sqrt，add,…这些，使用过math库的都懂的)，这里就不挨个说明了，在上方的思维导图中罗列了：

  1. 通用的ufunc
  2. 用于数据处理的ufunc
  3. 用于统计学的ufunc

大家结合图中的方法自己敲敲练练就OK了，这里只是要说明几点。

3.1 out 参数

ufunc一般是返回一个处理好的视图，也就是说ufunc并不会改变原数组。但是其可以接受一个out参数，用于作为输出参数，如下示例：

1
2
3
4
5
6
7
8
arr = np.array([16, 9, 4])
arr2 = np.sqrt(arr)
log('使用ufunc后的arr', arr)      #  [16, 9, 4]
log('看看np.sqrt的输出', arr2)    #   [4, 3, 2]

np.sqrt(arr, arr2)  # 使用 out 参数
log('使用out参数, 原数组arr', arr)   #  [16, 9, 4]
log('使用out参数，arr2', arr2)      #   [4, 3, 2]

像这样np.sqrt(arr, arr)，将out参数指为自己会报错，看来ufunc还是不愿意改变处理的数组本身。

注意，我们说的通用的ufunc都是np.xx这样的，比如求一个数组的平方根，是np.sqrt(arr)，而不能使用 arr.sqrt()

4 meshgrid 与 where

4.1 np.meshgird

1
2
3
4
5
#生成一维数组，其实也就是向量
x = np.arange(-2,2)  # 【-2，-1，0，1】
y = np.arange(0,3)   #  【0，1，2】

z,s = np.meshgrid(x,y) # 将两个一维数组变为二维矩阵

从输出的结果看:

meshgrid输出的结果分析
1
2
3
4
5
6
                      | y, y, y ,y|
-                     -------------
x： -2, -1,  0,  1      0, 0, 0, 0
x： -2, -1,  0,  1  --> 1, 1, 1, 1
x： -2, -1,  0,  1      2, 2, 2, 2
-        z矩阵              s矩阵

我们在上面把结果单独拎出来看，x变成了矩阵z的行向量，y变成了矩阵s的列向量。

这样的好处就是我们可以对此2向量运用矩阵乘法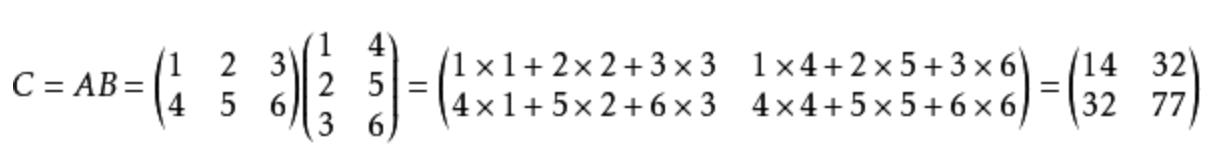
py-np-meshgrid

4.2 np.where

1
np.where(condition, [x, y])  # 当condition为True时返回x, 否则返回y

我们直接从具体的实例看下就好理解了

1
2
3
4
arr = np.arange(9).reshape(3,3)
print('--原矩阵-->\n',arr)
print('--where(arr > 4)-->\n',np.where(arr > 4))  ==> out: (array([1, 2, 2, 2]), array([2, 0, 1, 2]))
print('--where(arr > 4)-->\n',np.where(arr > 4, 'a', 'b'))

我们先使用 arange + reshage生成了一个普通矩阵：

原矩阵->np.arange(9).reshape(3,3)输出
1
2
3
0 1 2
3 4 5
6 7 8

where中只有条件没有给结果操作时，如np.where(arr > 4) 。输出：(array([1, 2, 2, 2]), array([2, 0, 1, 2]))。
意思是满足条件的元素索引。比如把上面返回的这两个数组这样放你就容易看明白了：

np.where(arr > 4)返回的结果
1
2
3
满足条件的元素位置：元素1， 元素2， 元素3， 元素4
                   1,      2,     2,     2
                   2,      0,     1,     2

我们看，arr[1,2]=5，满足>4;arr[2,0]=6,也满足>4…

np.where(arr > 4, ‘a’, ‘b’)就不是返回索引了，直接根据后面给的数据返回操作结果，有点像?:这个三元操作符：

1
2
3
'b' 'b' 'b'
'b' 'b' 'a'
'a' 'a' 'a'

大家可以照着原矩阵看看就明白了。

5 ndarray的统计学方法

对于统计学方法，numpy做的比较细致，你可以使用np方法，也在ndarray中实现了这样的成员级方法。比如求数组平均数：

使用np.mean(arr)和arr.mean()就是一样的。

6 文件存取

numpy中的文件存取比较简单，从导图中的api基本就可以了解了。

7 random方法

numpy.random模块对Py内置的random作了补充。其有两个主要特点：

  1. 因为生成的是伪随机数，所以速度快。
  2. 可以生成多种概率分布的样本值。

比如：

随机生成一个4*4的标准正态分布样本
1
2
3
4
5
6
7
samples = np.random.normal(size=(4,4)) # 随机生成一个4*4的标准正态分布样本

==> 4*4的标准正态分布样本
[[ 1.34479578 -0.08507317  0.24184596 -0.2014552 ]
 [ 0.94377666 -1.16010531  2.12713566 -1.52408138]
 [ 1.03350424  1.11857464 -2.8894401  -0.3529615 ]
 [-0.16497261  0.49361521  0.52624117 -0.44174049]]

7.1 numpy.random速度快

从上面的例子我们看出，使用 np.random 一次就可以生成整个样本值。而py内置的random一次只能生成一个值，要生成多个值时一般会使用循环。这也是我们说其速度快的原因。

7.2 随机种子

因为是伪随机数，所以可以通过随机种子防止样本重复。我们来大概了解下伪随机数与随机种子的关系。

  • 伪随机数与随机种子

伪随机数其实就是一堆早已生成好的随机数，我们后面再调用如randint方法获取随机数时，其实只是到这个早已生成好的随机数列表中取数而已。如果只有一张表，那就没有随机可言了，因为每次生成的随机数都是一样的。所以就有了随机种子，其实就是因为有多张随机数表，随机种子指定使用哪张表，就这么简单。

而为什么我们每次调随机方法获得的随机数是不一样的呢？这是因为从表中获取数据是有个index的，每次调用随机方法此index会自动后移，所以每次取得的随机数是不一样的。而每次设置随机种子时，这个index都会置回0.

  • 局部随机生成器

而使用np.random.seed(seedNum)会改变全局随机种子，我们要隔离全局状态的话，可以使用局部随机生成器，他将不受全局随机生成器的影响。

下面的示例展示了我所说的：

随机种子示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 2次使用相同的种子生成的随机数不一样，因为生成了一次后 index自动后移了
np.random.seed(123)
log(np.random.randint(1, 5, 5)) # [3 2 3 3 1]
log(np.random.randint(1, 5, 5)) # [3 3 2 4 3]

# 每次重新设置种子，index回到起点
np.random.seed(123)
log(np.random.randint(1, 5, 5)) # [3 2 3 3 1]
np.random.seed(123)
log(np.random.randint(1, 5, 5)) # [3 2 3 3 1]

# 局部随机生成器
rng = np.random.RandomState(123)
log(rng.randint(1, 5, 5))  # [3 2 3 3 1]
np.random.seed(123)  # 改变全局随机种子，不会影响全局随机种子
log(rng.randint(1, 5, 5)) # [3 3 2 4 3]

还有各种随机方法，具体情参见文章开头的思维导图。

8 小结

作为小结和对本章的练习，大家可以试着在纸上算算下面程序的输出，并亲自复制到源文件中执行对比看自己对了多少：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
# -*- coding: UTF-8 -*-

import numpy as np


def log(msgOrOjb, obj=None):
    """一个实用的log方法."""
    if isinstance(msgOrOjb, str):
        if obj is not None:
            print('\n==> ' + msgOrOjb + ':' , type(obj))
            print(obj)
        else:
            print('\n==> ' + msgOrOjb)
    else:
        print('\n==> ', type(msgOrOjb))
        print(msgOrOjb)
    print('----------')


def main():
    # ---  ufunc  ---
    arr = np.arange(3)
    log('创建原数组', arr)
    log('对数组内每个元素求平方', np.sqrt(arr))

    # out参数示例
    arr = np.array([16, 9, 4])
    arr2 = np.sqrt(arr)
    log('使用ufunc后的arr', arr)
    log('看看np.sqrt的输出', arr2)
    np.sqrt(arr, arr2)  # 使用 out 参数为自己
    log('使用out参数, 原数组arr', arr)
    log('使用out参数，arr2', arr2)

    # ---  numpy.random伪随机数  ---

    samples = np.random.normal(size=(4,4)) # 随机生成一个4*4的标准正态分布样本
    log('4*4的标准正态分布样本', samples)

    # 2次使用相同的种子生成的随机数不一样，因为生成了一次后 index自动后移了
    np.random.seed(123)
    log(np.random.randint(1, 5, 5)) # [3 2 3 3 1]
    log(np.random.randint(1, 5, 5)) # [3 3 2 4 3]

    # 每次重新设置种子，index回到起点
    np.random.seed(123)
    log(np.random.randint(1, 5, 5)) # [3 2 3 3 1]
    np.random.seed(123)
    log(np.random.randint(1, 5, 5)) # [3 2 3 3 1]

    # 局部随机生成器
    rng = np.random.RandomState(123)
    log(rng.randint(1, 5, 5))  # [3 2 3 3 1]
    np.random.seed(123)  # 改变全局随机种子，不会影响全局随机种子
    log(rng.randint(1, 5, 5)) # [3 3 2 4 3]

    log(np.random.randn(4,4))

if __name__ == '__main__':
    main()

9 引用

  1. 《利用python进行数据分析》 - WesMcKinney著，SeanCheney译 - WesMcKinney是pandas的开发者，所以必须是讲解numpy、pandas等数据处理工具最权威的专家了，他的这本书写的很简洁很易读，SeanCheney翻译的也是非常完美。十分值得推荐的。